第三章

概率分布

概率分布描述了随机变量取值的规律。

随机变量

随机变量是一个函数，它用数字来表示一个可能出现的事件。你可以定义你自己的随机变量，然后生成一些样本来观察它的经验分布。

点击或拉动选中右图中的一些六边形，然后在框中输入一个数字，点击提交，

颜色	数值
	0

生成你定义的随机变量的样本，观察相应的经验分布。

生成样本

重置

离散型和
连续型随机变量

常见的随机变量类型有两种：

离散型随机变量连续型随机变量

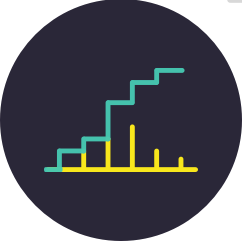
一个离散型随机变量可能的取值范围只有有限个或可列个值。离散型随机变量的定义是：如果$X$是一个随机变量，存在非负函数$f(x)$和$F(X)$,使得 $$ P(X=x) = f(x) \\ P(X < x) = F(x) $$ 则称$X$是一个离散型随机变量。

选择下方离散型随机变量，右图会出现它的概率质量函数$f(x)$（黄色）和分布函数$F(x)$（橙色）。调整滑块来改变分布函数。

如果一个随机变量$X$只取值$0$或$1$，概率分布是

$$P(X=1)=p,\quad P(X=0)=1-p$$

则称$X$符合伯努利分布(Bernoulli)。我们常用伯努利分布来模拟只有两种结果的试验，如抛硬币。

如果随机变量X是$n$个参数为$p$的独立伯努利随机变量之和，则称$X$是二项分布(binomial)。我们常用二项分布来模拟若干独立同分布的伯努利试验中的成功次数。比如说，抛五次硬币，其中正面的次数可以用二项分布来表示：Bin$(5,\dfrac{1}{2})$。

一个负二项分布的随机变量$X$表示的是若干独立同分布的参数为$p$的伯努利试验中获得$r$次失败前成功的次数。比方说，如果我们重复抛一枚硬币，我们则可以用负二项分布来表示抛出三次反面之前抛出正面的次数。

一个服从几何分布的随机变量表示了在重复独立同分布的伯努利试验中获得一次成功所需要的试验此时。比如说，如果我们重复投一枚骰子，我们则可以用几何分布来表示投出一个6所需要的试验次数。

泊松分布表示了一个事件在固定时间或者空间中发生的次数。泊松分布的参数$\lambda$是这个时间发生的频率。比方说，我们可以用泊松分布来刻画流星雨或者足球比赛中的进球数。

如果随机变量$X$在其支撑集上所有相同长度的区间上有相同的概率，即如果$b_1-a_1 = b_2-a_2$,则 $$P(X\in [a_1,b_1])=P(X\in [a_2,b_2]) $$ 那么我们称$X$服从均匀分布(Uniform)。比方说，我们一般可以假设人在一年中出生的概率是相等的，因此可以用均匀分布来模拟人的出生时间。

正态分布（也称高斯分布）的密度函数是一个钟形曲线。科学中常用正态分布来模拟许多小效应的叠加。比方说，我们知道人的身高是许多微小的基因和环境效应的叠加。因此可以用正态分布来表示人的身高，

学生t分布（也称t分布）往往在估计正态总体期望时出现。当我们只有较少的样本和未知的方差时，许多大样本性质并不适用，此时我们则需要用到t分布。

如果随机变量$X$是$k$个独立的标准正态随机变量的平方和，则称$X$是自由度为$k$的卡方随机变量：$X\sim \chi^2_k$. 卡方分布常见于假设检验和构造置信区间.

指数分布可以看作是几何分布的连续版本，其常用于描述等待时间。

F分布(Fisher–Snedecor分布)常在假设检验中出现，一个比较有名的例子是方差分析。

Gamma分布是一组连续型概率密度。指数分布和卡方分布是Gamma分布的两个特殊情形。

Beta分布是一族在$[0,1]$上的连续型概率分布，常用于贝叶斯统计中的共轭先验分布。

PMF 概率分布	期望	方差
$f(x;p) = \begin{cases} p & \text{if } x = 1 \\ 1-p & \text{if } x = 0 \end{cases}$ $ f(x; n,p) = \binom{n}{x}p^{x}(1-p)^{n-x}$ $f(x; n,r,p) = \binom{x + r -1}{x}p^{x}(1-p)^{r}$ $ f(x; p) = (1-p)^{x}p$ $ f(x;\lambda) = \dfrac{\lambda^{x}e^{-\lambda}}{x!}$ $f(x;a,b) = \left\{\begin{array}{ll} \dfrac{1}{b-a} \text{ for } x \in [a,b]\\ 0 \qquad \text{ otherwise } \end{array}\right.$ $ f(x;\mu, \sigma^2) = \dfrac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\dfrac{(x-\mu)^{2}}{2\sigma^{2}}}$ $\dfrac{Z}{\sqrt{U/k}} \qquad \begin{array}{ll} Z \sim N(0,1)\\ U \sim \chi_{k} \end{array}$ $\sum_{i=1}^{k}Z_{i}^{2} \qquad Z_{i} \overset{i.i.d.}{\sim} N(0,1)$ $ f(x;\lambda) = \begin{cases} \lambda e^{-\lambda x} & \text{if } x \geq 0 \\ 0 & \text{otherwise} \end{cases} $ $\dfrac{U_{1}/d_{1}}{U_{2}/d_{2}} \qquad \begin{array}{ll} U_{1} \sim \chi_{d_{1}}\\ U_{2} \sim \chi_{d_{2}} \end{array}$ $ f(x; k,\theta) = \dfrac{1}{\Gamma(k)\theta^{k}}x^{k-1}e^{-\dfrac{x}{\theta}}$ $f(x;\alpha,\beta) = \dfrac{\Gamma(\alpha + \beta)x^{\alpha - 1}(1-x)^{\beta - 1}}{\Gamma(\alpha)\Gamma(\beta)}$	$p$ $np$ $\dfrac{pr}{1-p}$ $\dfrac{1}{p}$ $\lambda$ $\dfrac{a+b}{2}$ $\mu$ $0$ $k$ $\frac{1}{\lambda}$ $\dfrac{d_{2}}{d_{2}-2}$ $k\theta$ $\dfrac{\alpha}{\alpha + \beta}$	$p(1-p)$ $np(1-p)$ $\dfrac{pr}{(1-p)^{2}}$ $\dfrac{1-p}{p^{2}}$ $\lambda$ $\dfrac{(b-a)^{2}}{12}$ $\sigma^{2}$ $\dfrac{k}{k-2}$ $2k$ $\frac{1}{\lambda^{2}}$ $\dfrac{2d_{2}^{2}(d_{1} + d_{2} -2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}$ $k\theta^{2}$ $\dfrac{\alpha\beta}{(\alpha + \beta)^{2}(\alpha + \beta + 1)}$

$\large p$ = 0.5

$\large n$ = 5
$\large p$ = 0.5

$\large r$ = 5
$\large p$ = 0.5

$\large p$ = 0.5

$\large\lambda$ = 5

$\large a$ = -5
$\large b$ = 5

$\large \mu$ = 0
$\large \sigma$ = 1

$\large k$ = 5

$\large \lambda$ = 5

$\large d_{1}$ = 5
$\large d_{2}$ = 5

$\large k$ = 5
$\large \theta$ = 5

$\large \alpha$ = 5
$\large \beta$ = 5

中心极限定理

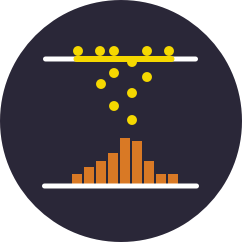
中心极限定理告诉我们，对于一个（性质比较好的）分布，如果我们有足够大的独立同分布的样本，其样本均值会（近似地）呈正态分布。样本数量越大，其分布与正态越接近。

你可以通过调节参数$\alpha$和$\beta$来改变概率分布。

$\large \alpha$ = 1.00
$\large \beta$ = 1.00

选择每组样本大小和抽取次数（样本均值的个数），然后点击“生成样本”。

样本大小 = 1
抽取次数 = 1

理论值

生成样本

图形展示改编自Philipp Plewa: 中心极限定理

下载英文PDF

第三章

概率分布

随机变量

离散型和连续型随机变量

中心极限定理

下一章

离散型和
连续型随机变量